Sistemas de Numeración
- Sistema Binario – Base 2
- Sistema Octal – Base 8 = 23
- Sistema Hexadecimal – Base 16 = 24
Sistema Binario
llamado también sistema diádico en ciencias de la computación, es un sistema de numeración en el que los números se representan utilizando solamente dos cifras: cero y uno (0 y 1). Es uno de los sistemas que se utilizan en las computadoras, debido a que estas trabajan internamente con dos niveles de voltaje, por lo cual su sistema de numeración natural es el sistema binario.
El sistema numérico en base 8 se llama octal y utiliza los dígitos del 0 al 7. En informática a veces se utiliza la numeración octal en vez de la hexadecimal. Tiene la ventaja de que no requiere utilizar otros símbolos diferentes de los dígitos. Sin embargo, para trabajar con bytes o conjuntos de ellos, asumiendo que un byte es una palabra de 8 bits, suele ser más cómodo el sistema hexadecimal, por cuanto todo byte así definido es completamente representable por dos dígitos hexadecimales.
Sistema Hexadecimal
es el sistema de numeración posicional que tiene como base el 16. Su uso actual está muy vinculado a la informática y ciencias de la computación donde las operaciones de la CPU suelen usar el byte u octeto como unidad básica de memoria; y, debido a que un byte representa valores posibles, y esto puede representarse como , que equivale al número en base 16 , dos dígitos hexadecimales corresponden exactamente a un byte.
Tabla de conversión

algunos ejemplos de Conversiones utilizando los tres sistemas:
Conversión de Binario a decimal
Conversión de Octal a decimal

Conversión de Hexadecimal a decimal
Operaciones Con binario
Al igual que en otros sistemas de numeración, también se pueden realizar operaciones con números binarios. Es decir que para este sistema binario que solo tiene dos símbolos en su lenguaje, también pueden hacerse ejercicios matemáticos y en este apartado se va a tratar el tema de las operaciones básicas de números binarios como es la suma, la resta, la multiplicación y la división, que aunque pueda parecer complicado, en realidad es algo bastante simples si se compara con las operaciones en el sistema decimal que es el de mayor uso en todo el mundo.
Suma Binaria
La aritmética binaria es muy similar a la aritmética decimal. Por ejemplo, para realizar una suma binaria hay que tener en cuenta la siguiente tabla:

| Ejemplo 1: Para sumar los números binarios 100102 y 1102 se puede escribir: |
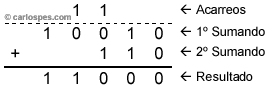 |
Resta Binaria
Si se quiere realizar una resta binaria se debe considerar la siguiente tabla:
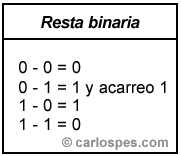
| Ejemplo 2: Para restar los números binarios 1010012 y 10112 escribiremos: |
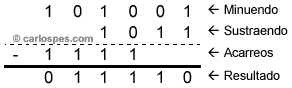 |
Multiplicación Binaria
| Para efectuar una multiplicación binaria se tiene que tener en cuenta la siguiente tabla: |
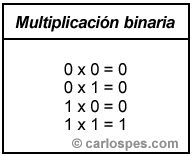 |
| Ejemplo 3: Para realizar el producto de los números binarios 101012 y 1012 hay que realizar los siguientes cálculos: |
 |
División Binaria
| En cuanto a las divisiones binarias, las reglas también son las mismas que en el Sistema Decimal, con la ventaja de que en binario sólo se usan dos dígitos. |
| Ejemplo 4: Para dividir 1100102 entre 102 los cálculos son: |
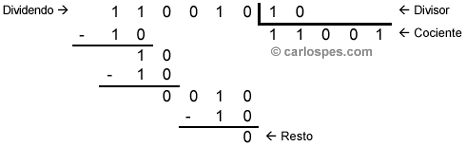 |
Complemento AI
El complemento A1 (UNO) de un número binario es el número resultante
de invertir los UNOS y CEROS del número binario.
Ejemplo:
110001 ----> 001110
001010 --------> 110101
Complemento A2
El
complemento A2 (DOS) consiste en sumar 1 (UNO) al complemento A1.
Ejemplos:
Obtener
el CA2 de 101010
◦CA1:
010101
◦CA2:
010101 + 1 = 010110
Método del CA2 al sustraendo
—La resta binaria de dos números
puede obtenerse sumando al minuendo el complemento a dos (CA2) del sustraendo.
—Se evita pedir prestado
repetidamente de una columna a otra en la resta.
—Permite conocer el signo del
resultado de una resta en el sistema binario.
Pasos Del Complemento A2 al sustraendo
1. Obtener el CA2 al sustraendo.
2. Al nuevo sustraendo sumar el minuendo.
3. Si se genera dígito de acarreo,
implica que el número es positivo y se deja el resultado tal como está.
4. Si no se genera dígito de acarreo,
implica que el número es negativo y se debe sacar el CA2 al resultado





No hay comentarios:
Publicar un comentario